Subtractive Mixture Models via Squaring: Representation and Learning
Published in ICLR 2024
Authors: Lorenzo Loconte, Aleksanteri M. Sladek, Stefan Mengel, Martin Trapp, Arno Solin, Nicolas Gillis, Antonio Vergari
Project URL: https://openreview.net/forum?id=xIHi5nxu9P
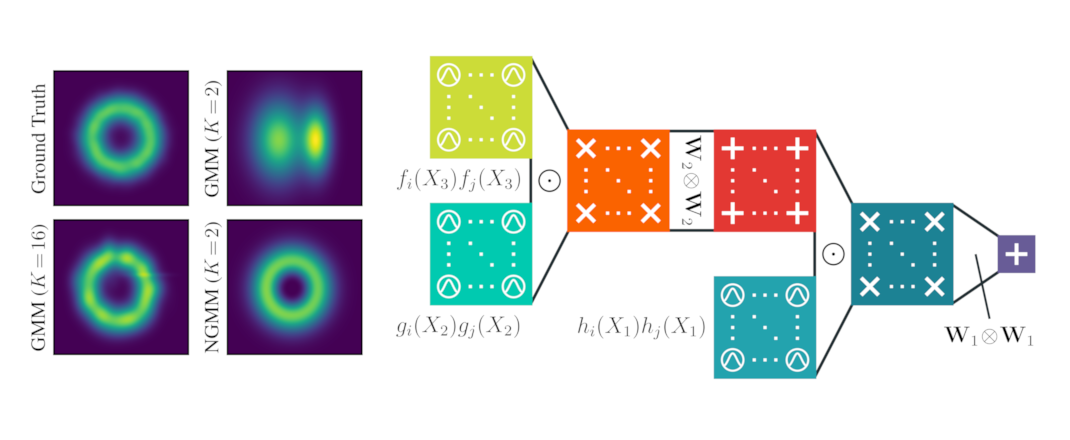
Abstract: Mixture models are traditionally represented and learned by adding several distributions as components. Allowing mixtures to subtract probability mass or density can drastically reduce the number of components needed to model complex distributions. However, learning such subtractive mixtures while ensuring they still encode a non-negative function is challenging. We investigate how to learn and perform inference on deep subtractive mixtures by squaring them. We do this in the framework of probabilistic circuits, which enable us to represent tensorized mixtures and generalize several other subtractive models. We theoretically prove that the class of squared circuits allowing subtractions can be exponentially more expressive than traditional additive mixtures; and, we empirically show this increased expressiveness on a series of real-world distribution estimation tasks.
Bibtex:
@inproceedings{loconte2024subtractive,
title={Subtractive Mixture Models via Squaring: Representation and Learning},
author={Loconte, Lorenzo and Aleksanteri, M. Sladek and Mengel, Stefan and Trapp, Martin and Solin, Arno and Gillis, Nicolas and Vergari, Antonio},
booktitle={The Twelfth International Conference on Learning Representations},
year={2024},
url={https://openreview.net/forum?id=xIHi5nxu9P}}